The paper found a statistically significant relationship (p=.034) between mean citalopram dose and effect size (see Figure 1 below) and went on to split the data into doses above and below 45mg and found that doses below 45mg (but not above) had a statistically significantly smaller effect size than the control antidepressants.
 |
| Figure 1. Regression from Aursnes et al 2010 |
It is very unclear from the paper what methods they used - it appears that they used standardised mean difference (SMD) in change scores but it is very unclear how they computed the change scores from the data they had available. The data they show for most studies does not report change scores and you wouldn't normally be able to estimate the standard deviation of this measure (which you need for the meta-analysis) unless the study reported the correlation between baseline and final score (which is very unlikely).***
Naturally I wanted to have a look at the data and regular readers of this blog will know that baseline severity is an important predictor of antidepressant efficacy in trials and I was interested to see what effect that would have in this study. Some of the source data is conveniently provided, it was obtained from Danish medicine licensing applications for citalopram so likely to be less subject to publication bias (in a similar way to the Kirsch et al data). I was able to get final score data for the studies using the Hamilton Rating Scale for Depression (HRSD-17) as outcome but had to impute standard deviations for those using the Montgomery-Åsberg Depression Rating Scale (MADRS). I could obtain change score SMD data from their figures but I think this is a little unreliable***. I used all the studies with an active comparator (usually a tricyclic antidepressant**). All analyses were random effects unless otherwise noted, and everything was done in R.
So the first thing I wanted to do was reproduce the correlation between mean dose of citalopram and effect size. Using the data I extracted (see Figure 2 below) my meta-regression showed a slope of .038 of SMD against citalopram dose (p=.13). Then I used their numbers (SMD and standard error) and performed another meta-regression. This showed a regression slope of .037 (similar, but not the same as their .038) but it was not statistically significant (p=.20) even if I used a fixed effects regression (p=.19). This is surprising as the authors report statistical significance at p=.034! The only way I can get their data to give a statistically significant regression is to include the placebo studies so that the slope is now .041 with p=.033 but this would be completely wrong. Having placebo studies included only for high doses of 50mg and 60mg will overestimate the effect of citalopram at high doses since we expect citalopram to be better than placebo but no better or worse than another antidepressant as control.
Performing multiple regression with dose and baseline score against weighted mean difference in HRSD score and MADRS score separately**** showed slopes of .73 (p=.10) and -.047 (p=.76) for baseline severity and mean dose respectively for HRSD scores and 1.06 (p=.30) and .25 (p=.75) for MADRS scores. So no statistically significant effect of baseline severity. That isn't necessarily surprising because it may be that both citalopram and other antidepressants are all equally affected by increasing efficacy with increasing severity of depression.
 |
| Figure 2. The data I have extracted presented as weighted mean differences in RevMan 5.0 |
So, in summary, there does not seem to be a robust relationship between the effect size of citalopram and the mean dose used in trials - I do not think a discrepancy of this magnitude is likely to due to methodological differences and I hypothesise that Aursnes et al (2010) have made a calculation error. Therefore it does not make sense to divide the studies based on citalopram dose. If we combine all studies using the SMD as outcome (see Figure 3 below) there is not a statistically significant difference between the citalopram and active control arms of trials although the difference is borderline significant (p=.057) and includes differences up to -.46 which corresponds to scores on the HRSD up to 4 points*****. It is worth bearing in mind that not a single trial had a mean dose of citalopram less than 40mg so this analysis cannot tell us much about lower doses of 20-30mg of citalopram and, if the correlation with dose is not real, then it can tell us nothing about these lower doses. In some ways this resembles the study by Kirsch et al where the authors used a regression analysis to make claims about patients with low severity by extrapolating the line into a region where there were not actually any studies.******
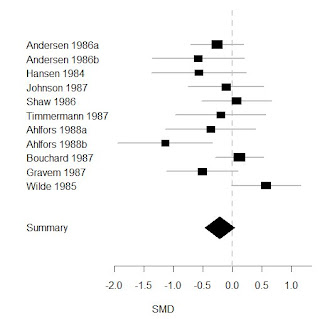 |
| Figure 3. All active control studies combined using SMD as outcome, to the left of 0.0 favours control and to the right favours citalopram |
* No study had a mean dose of citalopram less than 40mg.
** Two amitriptyline, two clomipramine, three mianserin, two maprotiline, nortripyline, and imipramine. The paper seems to misreport this but looking at the original data sheets they get their numbers from I think my numbers are right and their report of five studies using mianserin is wrong.
*** This is what the authors say about their methods:
These data were fed into a tailor-made program for performing meta-analysis (Comprehensive Meta-analysis Version 2, from Biostat, Englewood, USA), which uses standard statistical procedures [9]. We filled in columns for the mean score, its standard deviation, and the number of patients in the citalopram group and in the comparator group. We added a column for correlation between before and after, Pearson’s coefficient of correlation found to be 0.48, and standardized the effect analysis with standard deviations of the differences between values before and after. We found I2 to be 73.5 and performed random effect meta-analyses with the effects weighted with the inverse of their variances.And I think they've probably committed an error in their methodology because I'm not sure what they think that correlation is for - they can't use that (the between study correlation) to estimate the correlation between baseline and final scores within studies and then use that to calculate change score standard deviations. That would be completely wrong. It is also noteable that the authors do an 'intention to treat' analysis in addition to 'last observation carried forward' but this is a flawed approach for continuous measures if you don't have access to the original data and it inflates the apparent sample size and does not capture any useful information regarding drop-outs that 'intention to treat' does with dichotomous data.
**** They can't be combined together because the baseline scores are in HRSD or MADRS units respectively.
***** You can see from Figure 2 that the studies using the HRSD did show a statistically significant decrease in the citalopram group.
****** If the regression slope were to be taken seriously an arbitrary 'clinically significant' difference of .35 (around 3 points on the HRSD) is reached around a dose of 40mg.
3 comments:
Interesting post. Less than 2% of my patient take doses of Citalopram higher than 40mg day. So your analysis is reassuring.
Well, on the other hand, it doesn't provide any evidence for an antidepressant effect of 30mg or less of citalopram. The paper discusses other post-licensing studies of citalopram which I haven't gone into.
This is a really interesting post, thanks for this.
We really should try and poach you for the site as part of our grand wooing.
;)
Keir
Post a Comment